Reflecting on performance
I'm going to take a short break from Noir tutorials and do a post on optimization and profiling instead. I was playing around with rendering Metaballs and I stumbled on a neat visualization.

To get the above effect we simply calculate the influence of each metaball on each point on the screen based on the distances to each ball's center and radius:
imp = rmp / √ (δxmp2 + δymp2)
where r is the radius of the metabll and δxmp and δymp are the x and y distances from the center of the metaball
cp = Σ imp
The algorithm is on the order of
The code to accomplish this is as follows:
;;compute influence of each metaball
(defn influence [{:keys [x y radius]} px py]
(let [dx (- x px)
dy (- y py)]
(/ radius (Math/sqrt (+ (* dx dx) (* dy dy))))))
;;compute the resulting r g b values based on influence
(defn compute-color [x y [red-cur green-cur blue-cur] ball]
(let [influence (influence ball x y)
[r g b] (:color ball)]
[(+ red-cur (* influence r))
(+ green-cur (* influence g))
(+ blue-cur (* influence b))]))
...
;;reverse direction if we hit the edge of the screen
(defn direction [p v]
(if (or (> p SIZE) (neg? p)) (- v) v))
;;compute the position and velocity of the ball
(defn move [{:keys [x y vx vy radius color]}]
(let [vx (direction x vx)
vy (direction y vy)]
{:x (+ x vx)
:y (+ y vy)
:vx vx
:vy vy
:radius radius
:color color}))
;;for each x,y coordinate compute the color
(reduce (partial compute-color x y) [0 0 0] balls)
;;run this in a loop where we move the
;;balls around and render them
(loop [balls (take 2 (repeatedly metaball))]
(draw canvas balls)
(recur (map move balls)))
complete code can be seen here
First thing to do is to time our our loop:
(loop [balls (take 2 (repeatedly metaball))]
(time (draw canvas balls))
(recur (time (map move balls))))
"Elapsed time: 250.345 msecs"
"Elapsed time: 0.004 msecs"
"Elapsed time: 171.136 msecs"
"Elapsed time: 0.005 msecs"
"Elapsed time: 212.646 msecs"
"Elapsed time: 0.004 msecs"
As can be expected the draw function eclipses the move function. So we'll focus on what's happening in our rendering code and see where the CPU time is being spent. Instead of guessing, let's profile the application using VisualVM, which should already be bundled with your JVM, and see what's happening.
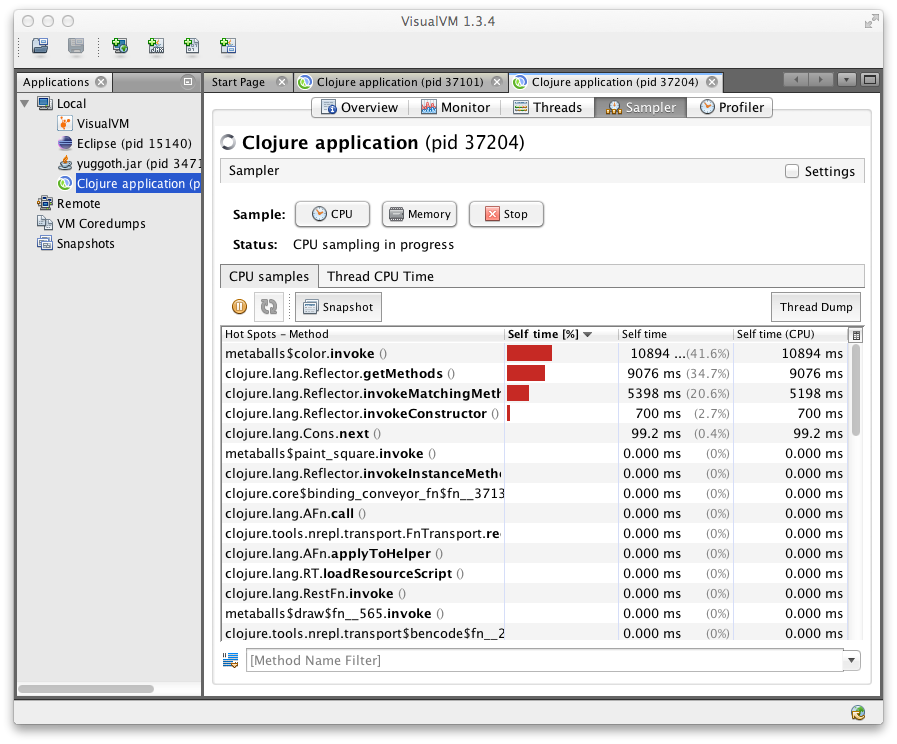
We can see that the vast majority of the CPU time is being spent in the color function, and that reflection is the culprit. So, let's see why reflection is happening by setting the *warn-on-reflection* flag to true:
(set! *warn-on-reflection* true)
Reflection warning, metaballs.clj:32 - call to java.awt.Color ctor can't be resolved.
Reflection warning, metaballs.clj:40 - call to setColor can't be resolved.
Reflection warning, metaballs.clj:40 - call to fillRect can't be resolved.
Reflection warning, metaballs.clj:52 - reference to field getBufferStrategy can't be resolved.
Reflection warning, metaballs.clj:53 - reference to field getDrawGraphics can't be resolved.
Reflection warning, metaballs.clj:64 - reference to field dispose can't be resolved.
Reflection warning, metaballs.clj:65 - reference to field contentsLost can't be resolved.
Reflection warning, metaballs.clj:66 - reference to field show can't be resolved.
Now we know precisely which spots are causing us trouble. Let's see if adding some annotations will improve things. First warning we hit happens when we create a new instance of Color:
(defn color-in-range [c]
(int
(cond
(< c 0) 0
(> c 255) 255
:default c)))
(defn color [r g b]
(new Color (color-in-range r) (color-in-range g) (color-in-range b)))
what's happening here is that even though we cast the result into int inside color-in-range, color is not aware of it and uses reflection to resolve the constructor for Color. So we should be doing the cast inside color instead:
(defn color [r g b]
(new Color (int (color-in-range r))
(int (color-in-range g))
(int (color-in-range b))))
The rest of the warnings simply require annotations for the classes in the function arguments:
(defn paint-square [g color x y size]
(doto g
(.setColor color)
(.fillRect x y size size)))
becomes
(defn paint-square [^Graphics g ^Color color x y size]
(doto g
(.setColor color)
(.fillRect x y size size)))
and so on. Finally, we'll cast our distances to doubles when we compute the influence:
(defn influence [{:keys [x y radius]} px py]
(let [dx (double (- x px))
dy (double (- y py))]
(double (/ radius (Math/sqrt (+ (* dx dx) (* dy dy)))))))
optimized version can be seen here
Now that we've annotated our code let's see if performance is any better:
"Elapsed time: 55.424 msecs"
"Elapsed time: 55.399 msecs"
"Elapsed time: 55.373 msecs"
"Elapsed time: 55.482 msecs"
Indeed it is, we went from ~200ms to ~55ms a 4X improvement in speed! Let's see what the profiler has to say now:
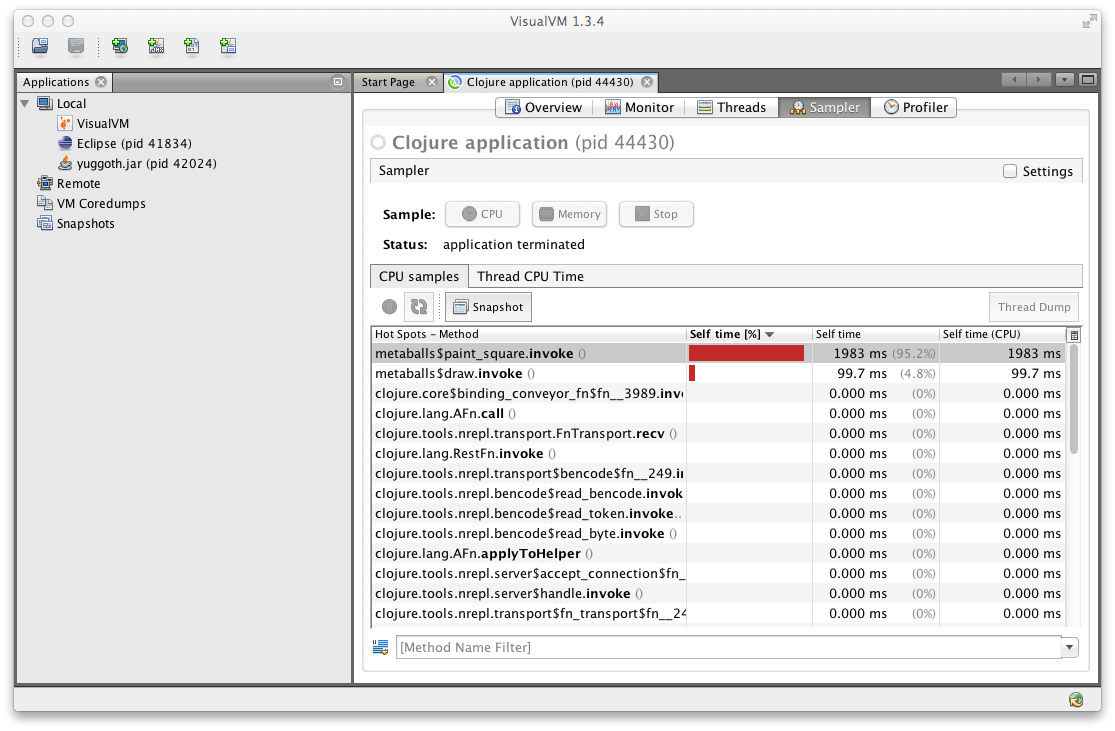
From here we can clearly see that majority of the time is spent in the paint-square function, meaning that our code performs as it should. Turns out the the only real factor on performance is reflection.
We could've spent time doing random optimizations here and there, but it's clear from profiling which functions are actually eating up the resources and need optimizing. While this is a toy project, the technique is equally effective for large projects where it might be much more difficult to guess which functions need tuning.
P.S. try setting a negative radius for some of the metaballs in the scene :P